Evaluer un algorithme approché

Nous avons déjà parlé de correction, de terminaison, de complexité… Mais pour les algorithmes approchés une autre notion importante est celle de précision.

Pourquoi des algorithmes approchés ?

Quand un algorithme doit répondre à un problème, il ne peut qu’avoir raison ou tort. Un algorithme approché ne donne pas nécessairement la réponse au problème, mais peut-être une réponse “acceptable”. En pratique trouver une réponse acceptable peut parfois se faire en un temps beaucoup moins important que de trouver la bonne réponse.

Les algorithmes approchés posent le problème du compromis performance-précision. Autrement dit : à quel point je gagne en vitesse d’exécution par rapport à ce que je perds en qualité de ma réponse ?

Précision d’un algorithme approché

Du fait de la très grande diversité des algorithmes et des données qu’ils manipulent, il est très difficile de donner un cadre formel universel à la notion de précision.

Prenons l’exemple d’un problème dont la solution est un entier. La précision d’un algorithme approché répondant à ce problème peut alors être l’écart moyen entre sa réponse et la bonne réponse attendue.

Comment évaluer la précision d’un algorithme approché ?

Déjà, pour évaluer la précision, il est nécessaire d’avoir une idée de la réponse attendue qui peut-être donnée par un algorithme exact. Ensuite l’idée est de tester un grand nombre de cas et d’en tirer des informations statistiques utiles.

Bien évidemment, il n’est pas forcément possible de se comparer à la réponse exacte (sinon on n’utiliserait pas d’algorithme approché mais l’algorithme exact correspondant). On peut alors évaluer la précision de l’algorithme approché en se basant sur des critères mathématiques, comme par exemple la connaissance de l’appartenance du résultat à un certain intervalle.

Exemple de la coloration de graphes

Algorithmes

Nous allons considérer un exemple. On appelle coloration d’un graphe la donnée d’un entier associé à chacun de ses sommets. Ces entiers sont appelés les couleurs des sommets. Ces entiers peuvent être identiques. Une coloration est dite propre si tous sommets reliés par une arête sont de couleurs différentes. Le nombre chromatique d’un graphe est le nombre minimum de couleurs qui apparaissent dans une coloration propre.

Ce problème est un exemple connu de problème NP-Complet. Une façon de le résoudre de façon exacte consiste à énumérer l’ensemble des colorations possibles à 1 couleur, puis 2 couleurs etc jusqu’à trouver une coloration propre.

Le code Python suivant résout le problème :

# Function to check if a coloring is correct
# A coloring is correct if no neighbours share a color
def checkColoring (graph, colors) :
    
    # We test the colors of every pair of connected nodes
    for node in range(len(graph)) : 
        for neighbor in graph[node] :
            if colors[node] == colors[neighbor] :
                return False
    return True

#############################################################

# Transforms a given decimal integer into a list of digits in any base
# Won't work for bases higher than 36
def toBase (value, base, nbDigits) :
    
    # Inner function to change the base
    def _toBase (value) :
        digits = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
        if value < base :
            return [digits[value]]
        else :
            #print(value // base)
            return _toBase(value // base) + [digits[value % base]]
    
    # We fill the list with 0s until it is of the correct size
    result = _toBase(value)
    return ["0" for i in range(nbDigits - len(result))] + result
    
#############################################################

# This function returns a coloring of the given graph using a minimum number of colors
def coloring (graph) :
    
    # We gradually increase the number of available colors
    for nbColors in range(1, len(graph) + 1) :
        
        # If considering K colors, solutions can be encoded in base K with numbers ranging from 0 to 3^K
        for potentialSolution in range(nbColors**len(graph)) :
            colors = toBase(potentialSolution, nbColors, len(graph))
            print("Nb colors:", nbColors, " - Test", potentialSolution, ":", repr(colors))
            if checkColoring(graph, colors) :
                return colors
    
###################################################################
 
# Test graph
graph = [[1, 2, 5], [0, 2, 5], [0, 1], [4, 5], [3, 5], [0, 1, 3, 4]]
result = coloring(graph)
print(repr(result))

# Function to check if a coloring is correct

# A coloring is correct if no neighbours share a color

def checkColoring (graph, colors) :

# We test the colors of every pair of connected nodes

for node in range(len(graph)) :

for neighbor in graph[node] :

if colors[node] == colors[neighbor] :

return False

return True

#############################################################

# Transforms a given decimal integer into a list of digits in any base

# Won't work for bases higher than 36

def toBase (value, base, nbDigits) :

# Inner function to change the base

def _toBase (value) :

digits = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"

if value < base :

return [digits[value]]

else :

#print(value // base)

return _toBase(value // base) + [digits[value % base]]

# We fill the list with 0s until it is of the correct size

result = _toBase(value)

return ["0" for i in range(nbDigits - len(result))] + result

#############################################################

# This function returns a coloring of the given graph using a minimum number of colors

def coloring (graph) :

# We gradually increase the number of available colors

for nbColors in range(1, len(graph) + 1) :

# If considering K colors, solutions can be encoded in base K with numbers ranging from 0 to 3^K

for potentialSolution in range(nbColors**len(graph)) :

colors = toBase(potentialSolution, nbColors, len(graph))

print("Nb colors:", nbColors, " - Test", potentialSolution, ":", repr(colors))

if checkColoring(graph, colors) :

return colors

###################################################################

# Test graph

graph = [[1, 2, 5], [0, 2, 5], [0, 1], [4, 5], [3, 5], [0, 1, 3, 4]]

result = coloring(graph)

print(repr(result))

Dans cet exemple, le graphe utilisé est le suivant (représenté sous forme d’un tableau de listes) :

012345

Si 0 correspond à bleu, 1 correspond à rouge et 2 correspond à vert, on a comme résultat la coloration suivante :

012345

Cet algorithme est très complexe et une solution approchée bien connue consiste à trier les sommets par nombre de voisins décroissant, à les colorer dans cet ordre en choisissant la plus petite couleur positive laissant la coloration propre. Cet algorithme approché est décrit ci-dessous :

# Constant used to represent non-colored nodes
NO_COLOR = -1

#############################################################

# Function to check if a coloring is correct
# A coloring is correct if no neighbours share a color
def checkColoring (graph, colors) :
    
    # We test the colors of every pair of connected nodes
    for node in range(len(graph)) :
        if colors[node] != NO_COLOR :
            for neighbor in graph[node] :
                if colors[node] == colors[neighbor] :
                    return False
    return True

#############################################################

# This function greedily tries to color the graph from highest degree node to lowest degree one
def greedyColoring (graph) :
    
    # Sorting nodes in descending degree order
    toSortGraph = [(i, graph[i]) for i in range(len(graph))]
    sortedGraph = sorted(toSortGraph, key = lambda node: len(node[1]), reverse = True)
    
    # Coloring
    colors = [NO_COLOR] * len(graph)
    for node, neighbors in sortedGraph :
        for color in range(len(graph)) :
            colors[node] = color
            if checkColoring(graph, colors) :
                break
    return colors
    
###################################################################
 
# Test graph
graph = [[1, 2, 5], [0, 2, 5], [0, 1], [4, 5], [3, 5], [0, 1, 3, 4]]
result = greedyColoring(graph)
print(repr(result))

# Constant used to represent non-colored nodes

NO_COLOR = -1

#############################################################

# Function to check if a coloring is correct

# A coloring is correct if no neighbours share a color

def checkColoring (graph, colors) :

# We test the colors of every pair of connected nodes

for node in range(len(graph)) :

if colors[node] != NO_COLOR :

for neighbor in graph[node] :

if colors[node] == colors[neighbor] :

return False

return True

#############################################################

# This function greedily tries to color the graph from highest degree node to lowest degree one

def greedyColoring (graph) :

# Sorting nodes in descending degree order

toSortGraph = [(i, graph[i]) for i in range(len(graph))]

sortedGraph = sorted(toSortGraph, key = lambda node: len(node[1]), reverse = True)

# Coloring

colors = [NO_COLOR] * len(graph)

for node, neighbors in sortedGraph :

for color in range(len(graph)) :

colors[node] = color

if checkColoring(graph, colors) :

break

return colors

###################################################################

# Test graph

graph = [[1, 2, 5], [0, 2, 5], [0, 1], [4, 5], [3, 5], [0, 1, 3, 4]]

result = greedyColoring(graph)

print(repr(result))

Cet algorithme est beaucoup moins complexe que le précédent, et permet de considérer de très grands graphes.

Simulations

Afin d’évaluer la qualité de notre algorithme approché, nous allons nous intéresser à deux choses : le temps de calcul d’un côté, et la précision de l’autre. Pour tester ces deux quantités, nous allons générer un grand nombre de graphes aléatoires en utilisant le programme suivant :

import math, random

# Random graph generation parameters
NB_NODES = 100
EDGE_PROBABILITY = math.log(NB_NODES) / NB_NODES

# Number of graphs to test
NB_TESTS = 10

# Generates an Erdos-Renyi graph
def generateGraph () :
    graph = []
    for i in range(NB_NODES) :
        graph.append([])
    for i in range(NB_NODES) :
        for j in range(i + 1, NB_NODES) :
            if random.random() < EDGE_PROBABILITY :
                graph[i].append(j)
                graph[j].append(i)
    return graph

# Running tests
colors = 0
for i in range(NB_TESTS) :
    colors = colors + max(greedyColoring(generateGraph())) + 1
print(colors / NB_TESTS)

import math, random

# Random graph generation parameters

NB_NODES = 100

EDGE_PROBABILITY = math.log(NB_NODES) / NB_NODES

# Number of graphs to test

NB_TESTS = 10

# Generates an Erdos-Renyi graph

def generateGraph () :

graph = []

for i in range(NB_NODES) :

graph.append([])

for i in range(NB_NODES) :

for j in range(i + 1, NB_NODES) :

if random.random() < EDGE_PROBABILITY :

graph[i].append(j)

graph[j].append(i)

return graph

# Running tests

colors = 0

for i in range(NB_TESTS) :

colors = colors + max(greedyColoring(generateGraph())) + 1

print(colors / NB_TESTS)

Un programme similaire est utilisé pour le test exhaustif.

Temps de calcul

Pour connaître les performances en temps, nous utilisons la fonction “time” de linux :

% /usr/bin/time python approche.py
3.37
15.88user 0.00system 0:15.89elapsed 99%CPU (0avgtext+0avgdata 9388maxresident)k
0inputs+0outputs (0major+1065minor)pagefaults 0swaps

% /usr/bin/time python approche.py

3.37

15.88user 0.00system 0:15.89elapsed 99%CPU (0avgtext+0avgdata 9388maxresident)k

0inputs+0outputs (0major+1065minor)pagefaults 0swaps

La première ligne : “3.37” est le résultat de notre algorithme. Ensuite on peut lire différents temps. Le premier : “15.88s” correspond au temps consommé par l’utilisateur sur votre machine pour cette tâche, le second : “0.00s” au temps utilisé par le système et le dernier “0:15.89″ au temps vraiment écoulé. C’est le premier qui nous intéresse ici. Sur beaucoup de systèmes, la commande time peut être utilisée directement et est équivalente à “/usr/bin/time -p”. Le résultat est alors présenté autrement :

% time python approche.py
3.37
real 16.19
user 16.19
sys 0.00

% time python approche.py

3.37

real 16.19

user 16.19

sys 0.00

Notons que ce temps prend en compte la génération des graphes. Une autre façon de procéder est d’utiliser directement des primitives de python.

Pour utiliser directement Python, une solution est de prendre le temps avant de lancer les simulations, et une fois simulé.

On modifie donc notre code :

import math, random, time

# Random graph generation parameters
NB_NODES = 100
EDGE_PROBABILITY = math.log(NB_NODES) / NB_NODES

# Number of graphs to test
NB_TESTS = 10

# Generates an Erdos-Renyi graph
def generateGraph () :
    graph = []
    for i in range(NB_NODES) :
        graph.append([])
    for i in range(NB_NODES) :
        for j in range(i + 1, NB_NODES) :
            if random.random() < EDGE_PROBABILITY :
                graph[i].append(j)
                graph[j].append(i)
    return graph

# Generating graphs before running simulations
graphs = []
for i in range(NB_TESTS) :
    graphs.append(generateGraph())
    
# Running tests
timeStart = time.time()
colors = 0
for i in range(NB_TESTS) :
    colors = colors + max(greedyColoring(graphs[i])) + 1
elapsed = time.time () - timeStart
print(colors / NB_TESTS, elapsed)

import math, random, time

# Random graph generation parameters

NB_NODES = 100

EDGE_PROBABILITY = math.log(NB_NODES) / NB_NODES

# Number of graphs to test

NB_TESTS = 10

# Generates an Erdos-Renyi graph

def generateGraph () :

graph = []

for i in range(NB_NODES) :

graph.append([])

for i in range(NB_NODES) :

for j in range(i + 1, NB_NODES) :

if random.random() < EDGE_PROBABILITY :

graph[i].append(j)

graph[j].append(i)

return graph

# Generating graphs before running simulations

graphs = []

for i in range(NB_TESTS) :

graphs.append(generateGraph())

# Running tests

timeStart = time.time()

colors = 0

for i in range(NB_TESTS) :

colors = colors + max(greedyColoring(graphs[i])) + 1

elapsed = time.time () - timeStart

print(colors / NB_TESTS, elapsed)

Génération des courbes

Afin d’automatiser tout cela, nous allons passer les arguments par ligne de commande au programme python. Il suffit de modifier les lignes :

# Random graph generation parameters
NB_NODES = int(sys.argv[1])
EDGE_PROBABILITY = math.log(float(NB_NODES)) / float(NB_NODES)

# Number of graphs to test
NB_TESTS = int(sys.argv[2])

# Random graph generation parameters

NB_NODES = int(sys.argv[1])

EDGE_PROBABILITY = math.log(float(NB_NODES)) / float(NB_NODES)

# Number of graphs to test

NB_TESTS = int(sys.argv[2])

Maintenant on peut directement fournir la taille du graphe et le nombre de tests au programme :

% python approche.py 100 10
100 3.4 1.5700342655181885

% python approche.py 100 10

100 3.4 1.5700342655181885

On va maintenant lancer un script pour générer notre courbe :

% for n in {1..10}; do python approche.py ${n}0 100 >> results.txt ; done

1	% for n in {1..10}; do python approche.py ${n}0 100 >> results.txt ; done

Il ne reste plus qu’à l’afficher !

Exemple avec Gnuplot :

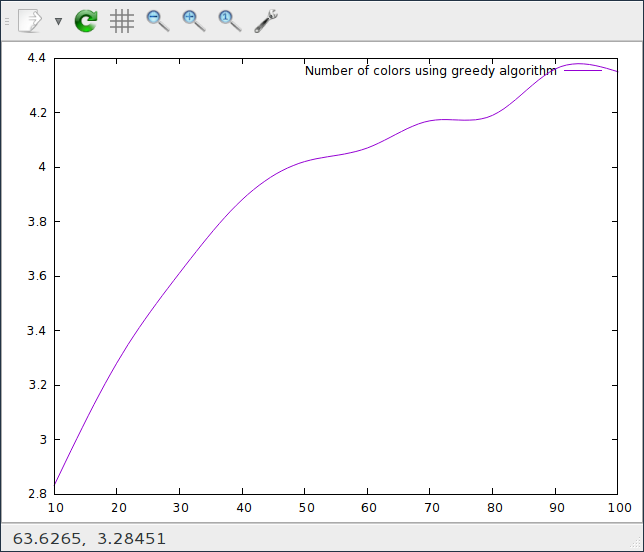
% gnuplot

	G N U P L O T
	Version 5.0 patchlevel 0    last modified 2015-01-01 

	Copyright (C) 1986-1993, 1998, 2004, 2007-2015
	Thomas Williams, Colin Kelley and many others

	gnuplot home:     http://www.gnuplot.info
	faq, bugs, etc:   type "help FAQ"
	immediate help:   type "help"  (plot window: hit 'h')

Terminal type set to 'qt'
gnuplot> plot "results.txt" using 1:2 title "Number of colors using greedy algorithm" with lines smooth csplines

% gnuplot

G N U P L O T

Version 5.0 patchlevel 0 last modified 2015-01-01

Thomas Williams, Colin Kelley and many others

gnuplot home: http://www.gnuplot.info

faq, bugs, etc: type "help FAQ"

immediate help: type "help" (plot window: hit 'h')

Terminal type set to 'qt'

gnuplot> plot "results.txt" using 1:2 title "Number of colors using greedy algorithm" with lines smooth csplines

On obtient ceci :

On remarque que la courbe n’est pas très lisse, c’est parce qu’un nombre insuffisant de simulations ont été faites.

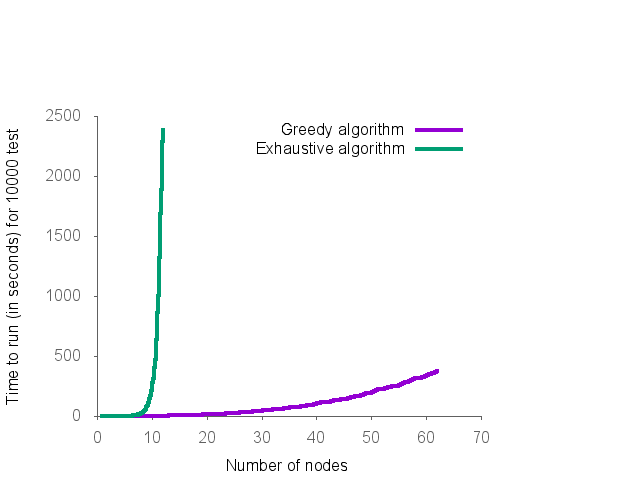
Au final, on obtient les courbes suivantes :

On remarque que ces courbes ne mettent pas vraiment en avant l’erreur faite par l’algorithme approché. Le soucis étant que faire tourner l’algorithme exhaustif sur de gros graphes demanderait trop de temps de calcul.

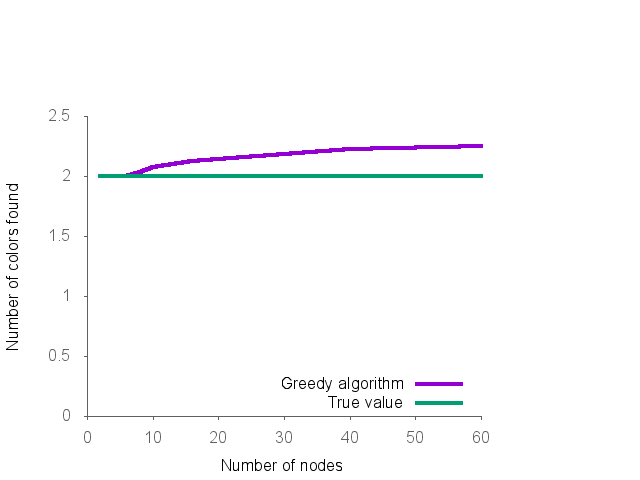
Pour mieux évaluer l’erreur de l’algorithme approché, on se propose donc de le faire tourner sur des graphes dont on connaît mathématiquement le nombre chromatique : des graphes bipartis. En effet les graphes bipartis possédant au moins une arête ont un nombre chromatique égal à deux.

On obtient les courbes suivantes :

Ces courbes ont été générées avec le script Gnuplot suivant :

# Header 
set encoding utf8

# Labels
set xlabel "Number of nodes"
set ylabel "Time to run (in seconds) for 10000 test"
set style line 11 lc rgb '#606060' lt 1
set border 3 back ls 11
set tics nomirror out scale 0.75

# Zoom
set size 0.8,0.8

# Lines definitions
set linestyle 1 lt 1 lw 4
set linestyle 2 lt 2 lw 4

# Output options
set term png
set output "time.png"

# Position the captions
set key top right

plot "greedy.txt" using 1:3 title "Greedy algorithm" with lines smooth csplines ls 1, "exhaustive.txt" using 1:3 title "Exhaustive algorithm" with lines smooth csplines ls 2

set ylabel "Number of colors found"
set output "precision.png"

set key bottom right

plot "greedy.txt" using 1:2 title "Greedy algorithm" with lines smooth csplines ls 1, "exhaustive.txt" using 1:2 title "Exhaustive algorithm" with lines smooth csplines ls 2

# Output options
set ylabel "Number of colors found"
set output "precisionbipartite.png"

# The following command allows to draw from y=0
set yrange [0:]
plot "greedybipartite.txt" using 1:2 title "Greedy algorithm" with lines ls 1, 2 title "True value" ls 2

# Output options
set term png
set output "timebipartite.png"

set ylabel "Time to run (in seconds) for 10000 test"

plot "greedybipartite.txt" using 1:3 title "Greedy algorithm" with lines smooth csplines ls 1

# Header

set encoding utf8

# Labels

set xlabel "Number of nodes"

set ylabel "Time to run (in seconds) for 10000 test"

set style line 11 lc rgb '#606060' lt 1

set border 3 back ls 11

set tics nomirror out scale 0.75

# Zoom

set size 0.8,0.8

# Lines definitions

set linestyle 1 lt 1 lw 4

set linestyle 2 lt 2 lw 4

# Output options

set term png

set output "time.png"

# Position the captions

set key top right

plot "greedy.txt" using 1:3 title "Greedy algorithm" with lines smooth csplines ls 1, "exhaustive.txt" using 1:3 title "Exhaustive algorithm" with lines smooth csplines ls 2

set ylabel "Number of colors found"

set output "precision.png"

set key bottom right

plot "greedy.txt" using 1:2 title "Greedy algorithm" with lines smooth csplines ls 1, "exhaustive.txt" using 1:2 title "Exhaustive algorithm" with lines smooth csplines ls 2

# Output options

set ylabel "Number of colors found"

set output "precisionbipartite.png"

# The following command allows to draw from y=0

set yrange [0:]

plot "greedybipartite.txt" using 1:2 title "Greedy algorithm" with lines ls 1, 2 title "True value" ls 2

# Output options

set term png

set output "timebipartite.png"

set ylabel "Time to run (in seconds) for 10000 test"

plot "greedybipartite.txt" using 1:3 title "Greedy algorithm" with lines smooth csplines ls 1

Evaluer un algorithme approché

Pourquoi des algorithmes approchés ?

Précision d’un algorithme approché

Comment évaluer la précision d’un algorithme approché ?

Exemple de la coloration de graphes

Algorithmes

Simulations

Temps de calcul

Génération des courbes

Pour approfondir

Laisser un commentaire Annuler la réponse.