Les tableaux
Les tableaux sont des structures servant à stocker un nombre fixe d’éléments. Chaque cellule d’un tableau est accessible par un indice, c’est à dire en quelques sortes sont adresse dans le tableau.
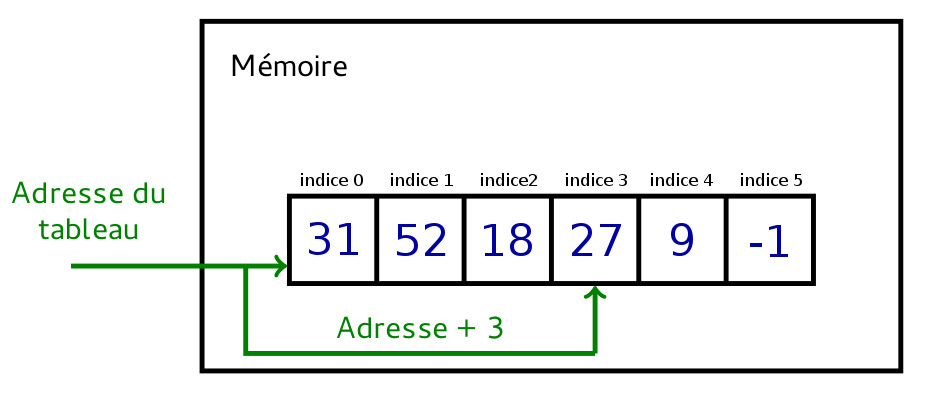
Il faut faire attention à ne pas confondre l’indice d’une cellule avec son contenu. Par exemple, soit t un tableau contenant six entiers : 31, 52, 18, 27, 9, -1. La première cellule de t (d’indice 0) contient la valeur 31, la seconde (d’indice 1) contient la valeur 52, etc.
Accéder au contenu (ou le modifier) d’une cellule du tableau est très simple, et extrêmement rapide : il suffit d’aller à l’indice désiré. Souvent, on note t[i], où t est un tableau, et i est un indice.
Ceci est possible car les cellules d’un tableau sont contiguës en mémoire. Accéder à t[i] revient donc à aller à l’adresse de t puis d’avancer de i cases.
Les listes
Contrairement aux tableaux, les listes ont une longueur variable. C’est à dire qu’on peut ajouter des éléments à une liste ou en supprimer. Une conséquence de cela est qu’on ne peut pas accéder aux éléments d’une liste par un indice aussi facilement que pour un tableau.
En effet, si les listes étaient faites comme les tableaux, supprimer une cellule en plein milieu causerait l’apparition d’un trou dans la structure de données. On pourrait corriger le problème en déplaçant tous les éléments siués à la droite du trou (dans les indices supérieurs) d’un cran à gauche, mais ce serait particulièrement long.
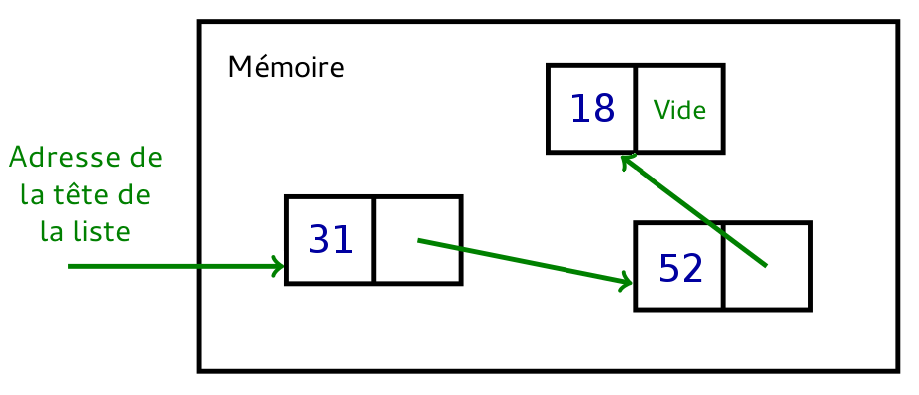
On préférera donc plutôt utiliser une structure de données différente. La principale différence entre un tableau et une liste est que les cellules de la liste ne sont pas contiguës en mémoire (d’où l’impossibilité d’accéder directement à une cellule par son indice). Ici, on considère que chaque cellule de la liste est un élément plus complexe, qui stocke d’une part une donnée et d’autre part un lien (appelé pointeur) vers la cellule suivante.
L’accès à la cellule d’indice i se fait donc en suivant i-1 fois les pointeurs vers la cellule suivante en partant d’une cellule initiale appelée tête de liste (on appelle les autres la queue de la liste).
Accéder à un élément en particulier est donc plus long que pour un tableau. En revanche, il est à présent aisé de supprimer une cellule ou d’en ajouter une nouvelle (il suffit de changer les liens entre les cellules).
Remarque : En Python, les listes l = [] sont un peu particulières. En effet, si ce sont bien des structures à taille variable, il est toutefois possible d’accéder à la case d’indice i via la fonction [], c’est à dire en écrivant l[i].
Les tables de hachage
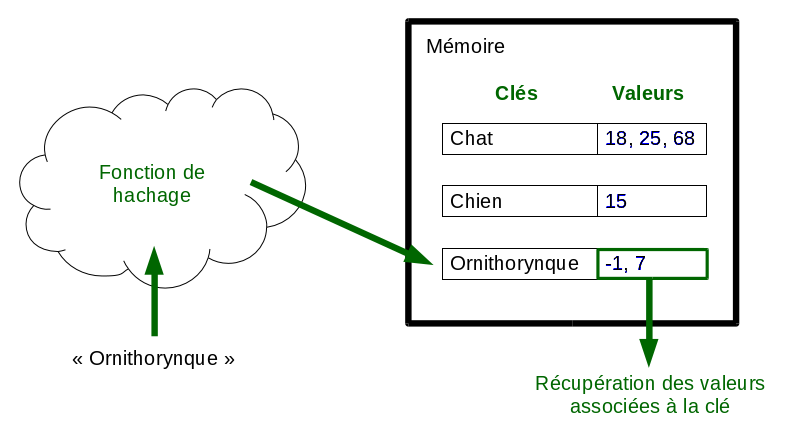
Les tables de hachage, aussi appelées dictionnaires, sont des structures de données bien pratiques. Elles permettent d’associer simplement des valeurs à des clés via une fonction appelée fonction de hachage. Si cette fonction de hachage est bien faite, accéder à une valeur (ou à un ensemble de valeurs) associée à une clé connue est très rapide.
Dans le cas de PyRat, vos programmes reçoivent la carte du labyrinthe sous la forme d’une table de hachage qui à chaque case (clé) associe une seconde table de hachage des voisins. Dans cette seconde table de hachage, la clé est la position du voisin, et la valeur le nombre de mouvements nécessaires pour y arriver. Ainsi, si map est la carte du labyrinthe, p1 est une position, et p2 est une position voisine de p1, on obtient le poids séparant p1 et p2 par map[p1][p2].