Illustrer un point avec des statistiques

L’informatique est une science difficile : les notions sont souvent extraites des mathématiques discrètes et prouver des résultats intuitifs peut être complexe. Plutôt que de prouver par l’outil mathématique une propriété, il arrive souvent que celles-ci soient appuyées par des simulations nombreuses et bien pensées. Dans cet article, nous prenons un exemple et nous montrons comment mettre en place une démarche scientifique pour analyser le problème.

Problème

Le problème que nous considérons ici est celui de la célèbre suite de Syracuse (dont il est aussi question sur cette fiche).

Une suite de Syracuse est obtenue par récurrence de la façon suivante :

Le premier terme est un paramètre u₀, entier strictement positif
Le terme u_i+1 est calculé comme suit :
- Si u_i est pair alors u_i+1 = u_i / 2
- Sinon u_i+1 = 3u_i + 1

À partir du moment où un 1 est rencontré dans cette suite, le cycle 1,4,2,1,4,2,… se répète indéfiniment.

On conjecture que pour tout choix de u₀, la suite va finir par passer par 1 et donc répéter ce cycle. Nul ne sait le prouver cependant.

Nous allons chercher à analyser l’impact de u₀ sur le nombre de valeurs que prend la suite avant de rencontrer la valeur 1.

Programme Python

Afin de réaliser ce travail, nous allons utiliser le programme python suivant :

# The syracuse function takes as an argument an integer n strictly higher than 0
# It outputs the number of steps before encountering 1
def syracuse (n) :
  if n == 1 :
    return 0
  else :
    if n % 2 == 0 :
      return 1 + syracuse(n / 2)
    else :
      return 1 + syracuse(3 * n + 1)

# The syracuse function takes as an argument an integer n strictly higher than 0

# It outputs the number of steps before encountering 1

def syracuse (n) :

if n == 1 :

return 0

else :

if n % 2 == 0 :

return 1 + syracuse(n / 2)

else :

return 1 + syracuse(3 * n + 1)

Nous allons enregistrer cette fonction dans un fichier nommé syracuse.py.

Petites valeurs de u₀

Dans un premier temps, nous allons regarder ce qu’il se passe avec de petites valeurs de u₀. Pour cela, nous allons rendre notre programme interfaçable avec un script, c’est-à-dire rendre facile son exécution avec différents paramètres.

On utilise pour cela le module sys de Python :

import sys

# We retrieve the first argument as u0
u0 = int(sys.argv[1])

# The syracuse function takes as an argument an integer n strictly higher than 0
# It outputs the number of steps before encountering 1
def syracuse (n) :
  if n == 1 :
    return 0
  else :
    if n % 2 == 0 :
      return 1 + syracuse(n / 2)
    else :
      return 1 + syracuse(3 * n + 1)

# We execute the function and output its result
print(syracuse(u0))

import sys

# We retrieve the first argument as u0

u0 = int(sys.argv[1])

# The syracuse function takes as an argument an integer n strictly higher than 0

# It outputs the number of steps before encountering 1

def syracuse (n) :

if n == 1 :

return 0

else :

if n % 2 == 0 :

return 1 + syracuse(n / 2)

else :

return 1 + syracuse(3 * n + 1)

# We execute the function and output its result

print(syracuse(u0))

Grâce à ce module, on peut maintenant lancer l’exécution de notre programme en mettant u₀ en argument. Pour ce faire, nous écrivons dans un terminal :

$ python3 syracuse.py 14

1	$ python3 syracuse.py 14

Nous pouvons alors lire en sortie 17.

Des résultats moyennés

Nous allons demander l’exécution de notre script pour toutes les premières valeurs de u₀ afin de voir comment évolue son comportement. Toujours dans un terminal, nous écrivons :

$ for i in {1..100}; do python3 syracuse.py $i; done

1	$ for i in {1..100}; do python3 syracuse.py $i; done

La sortie n’est pas très lisible… À la place nous préférerions avoir une courbe. Pour cela, nous allons créer un fichier au format .csv avec le résultat en fonction de u₀. Modifions l’affichage du résultat dans le fichier syracuse.py :

print(u0, syracuse(u0))

1	print(u0, syracuse(u0))

La ligne de commande dans le terminal devient comme suit, où >> results.csv permet de rediriger la sortie du programme vers le fichier results.csv :

$ rm -f results.csv
$ for i in {1..100}; do python3 syracuse.py $i >> results.csv; done

1 2	$ rm -f results.csv $ for i in {1..100}; do python3 syracuse.py $i >> results.csv; done

Pour lire ces données, nous écrivons dans le terminal :

$ libreoffice results.csv

1	$ libreoffice results.csv

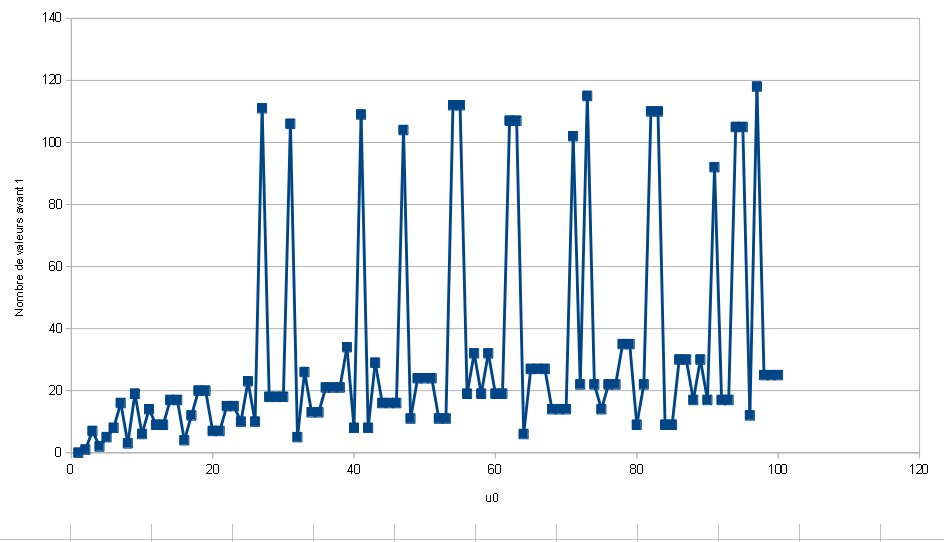
Nous cochons que les données sont séparées par des espaces et nous pouvons alors tracer la courbe suivante :

Analyse du comportement

Ce que nous avons déjà obtenu est intéressant, il semble que globalement notre courbe soit croissante même s’il y a de fortes variations locales.

Afin de vérifier cette affirmation, nous proposons d’aller voir pour de plus grandes valeurs de u₀ pour analyser la situation. Nous ne pouvons pas être exhaustif donc nous allons regarder ce qui se passe pour les premiers multiples de 1.000.000. Le problème est qu’étant données les variations, nous ne pouvons pas nous contenter de tracer une courbe avec un point pour chaque multiple de 1.000.000.

Ce que nous proposons alors est de regarder un grand nombre de nombres proches des multiples de 1.000.000 et d’en faire la moyenne. Pour cela, nous allons utiliser le module random de Python :

import random

# We perform 10.000 tests
TESTS = 10000

# We study a neighborhood of ± 50.000 around u0
NEIGHBORHOOD = 50000

# We start the computations and store the results in total
total = 0
for _ in range(TESTS) :
    total = total + syracuse(u0 + random.randint(-NEIGHBORHOOD, NEIGHBORHOOD))

# We write the output
print(u0, total / TESTS)

import random

# We perform 10.000 tests

TESTS = 10000

# We study a neighborhood of ± 50.000 around u0

NEIGHBORHOOD = 50000

# We start the computations and store the results in total

total = 0

for _ in range(TESTS) :

total = total + syracuse(u0 + random.randint(-NEIGHBORHOOD, NEIGHBORHOOD))

# We write the output

print(u0, total / TESTS)

En lançant plusieurs fois les tests avec :

$ python3 syracuse.py 1000000

1	$ python3 syracuse.py 1000000

on remarque que les valeurs ne changent pas beaucoup, ce qui veut dire que 10.000 tests pour chaque valeur est raisonnable.

Il nous reste à calculer le résultat pour nos différentes valeurs, et à écrire le résultat dans un fichier results.csv :

$ rm -f results.csv
$ for i in {1..100}; do python3 syracuse.py ${i}000000 >> results.csv; done

1 2	$ rm -f results.csv $ for i in {1..100}; do python3 syracuse.py ${i}000000 >> results.csv; done

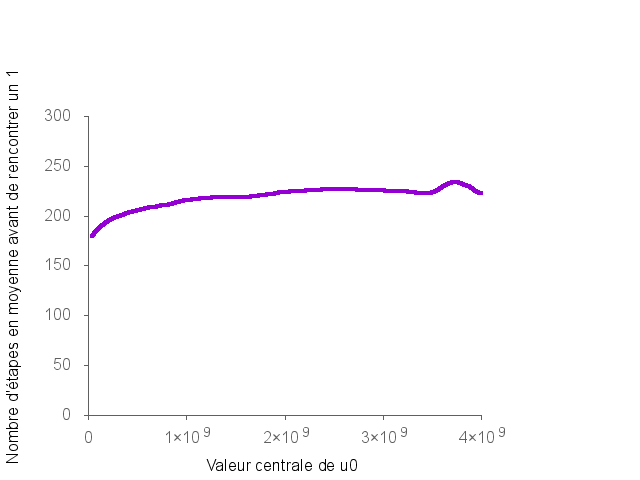
Ce script prend un peu de temps, ce qui est normal vu la quantité de calculs demandés. On obtient la courbe suivante :

Optimisons le programme

Plutôt que de tout recalculer à chaque fois, on peut placer en mémoire les résultats déjà obtenus pour accélérer les calculs. Ceci se fait aux dépends d’une consommation mémoire beaucoup plus importante (et potentiellement trop importante pour vos ordinateurs : si votre ordinateur tombe à court de mémoire, il va utiliser le SWAP ou pire encore, il va figer. N’hésitez pas à interrompre le programme en appuyant sur CTRL+C en cas de soucis) :

import sys

# We retrieve the first argument as u0
u0 = int(sys.argv[1])

# The idea is to fill a dictionary to count the number of values
# before a 1 is encountered, and to refer to them instead of computing
# everything again for other values
values = {1:0}

# Now, finding the requested value can be done either by consulting the dictionary,
# or by computing it if not present
def syracuse (n) :
    if n in values.keys() :
        return values[n]
    else :
        if n % 2 == 0 :
            res = 1 + syracuse(int(n / 2))
        else :
            res = 1 + syracuse(3 * n + 1)
    values[n] = res
    return res

# Function to compute everythig for a given u0
def computations (u0) :

    # We compute the mean for a certain neighborhood
    # Remark: here, we compute exhaustively in the neighborhood rather than using a random function
    NEIGHBORHOOD = 50000

    # We start the computations and store the results in total
    total = 0
    for i in range(NEIGHBORHOOD) :
        total = total + syracuse(u0 + i) + syracuse(u0 - i)

    return total / 2 / NEIGHBORHOOD

# We write the output
print(u0, computations(u0))

import sys

# We retrieve the first argument as u0

u0 = int(sys.argv[1])

# The idea is to fill a dictionary to count the number of values

# before a 1 is encountered, and to refer to them instead of computing

# everything again for other values

values = {1:0}

# Now, finding the requested value can be done either by consulting the dictionary,

# or by computing it if not present

def syracuse (n) :

if n in values.keys() :

return values[n]

else :

if n % 2 == 0 :

res = 1 + syracuse(int(n / 2))

else :

res = 1 + syracuse(3 * n + 1)

values[n] = res

return res

# Function to compute everythig for a given u0

def computations (u0) :

# We compute the mean for a certain neighborhood

# Remark: here, we compute exhaustively in the neighborhood rather than using a random function

NEIGHBORHOOD = 50000

# We start the computations and store the results in total

total = 0

for i in range(NEIGHBORHOOD) :

total = total + syracuse(u0 + i) + syracuse(u0 - i)

return total / 2 / NEIGHBORHOOD

# We write the output

print(u0, computations(u0))

On appelle le programme avec de grandes valeurs :

$ rm -f results.csv
$ for i in {1..100}; do echo $i; python3 syracuseopt.py $[ $i * 4 * 10000000 ] >> results.csv; done

1 2	$ rm -f results.csv $ for i in {1..100}; do echo $i; python3 syracuseopt.py $[ $i * 4 * 10000000 ] >> results.csv; done

On obtient la courbe suivante :

Cette courbe a été obtenue grâce à l’outil Gnuplot et au script suivant :

# Header         
set encoding utf8

# Labels
set xlabel "Valeur centrale de u0"
set ylabel "Nombre d'étapes avant de rencontrer un 1"
set style line 11 lc rgb '#606060' lt 1
set border 3 back ls 11
set tics nomirror out scale 0.75

# Ranges
set yrange [0:]

# Tics
set xtics 1000000000

# Zoom
set size 0.8,0.8

# Caption position
set key at 0.7,0.95

# Output options
set terminal png
set output "syracuse.png"

# Lines definitions
set linestyle 1 lt 1 lw 4

# Plot
plot "results.csv" using 1:2 notitle with linespoints ls 1 smooth bezier

# Header

set encoding utf8

# Labels

set xlabel "Valeur centrale de u0"

set ylabel "Nombre d'étapes avant de rencontrer un 1"

set style line 11 lc rgb '#606060' lt 1

set border 3 back ls 11

set tics nomirror out scale 0.75

# Ranges

set yrange [0:]

# Tics

set xtics 1000000000

# Zoom

set size 0.8,0.8

# Caption position

set key at 0.7,0.95

# Output options

set terminal png

set output "syracuse.png"

# Lines definitions

set linestyle 1 lt 1 lw 4

# Plot

plot "results.csv" using 1:2 notitle with linespoints ls 1 smooth bezier

Pour approfondir

Documentation de l’outil Gnuplot

Problème

Programme Python

Petites valeurs de u0

Des résultats moyennés

Analyse du comportement

Optimisons le programme

Pour approfondir

Laisser un commentaire Annuler la réponse.

Petites valeurs de u₀