Définition
Pour bien comprendre cette structure de données, imaginez un arbre (si si). Le tronc porte les premières branches, qui elles-même portent des branches plus petites (etc.), et au bout, on trouve des feuilles. Pour la structure de données, c’est pareil, à ceci près qu’on représente généralement les feuilles en bas et la base en haut.
Plus formellement, un arbre est simplement un graphe connexe, simple, et acyclique. Un tel graphe a naturellement une forme d’arbre (avec un peu d’imagination), d’où le nom.
On nomme généralement les différents éléments d’un arbre comme suit :
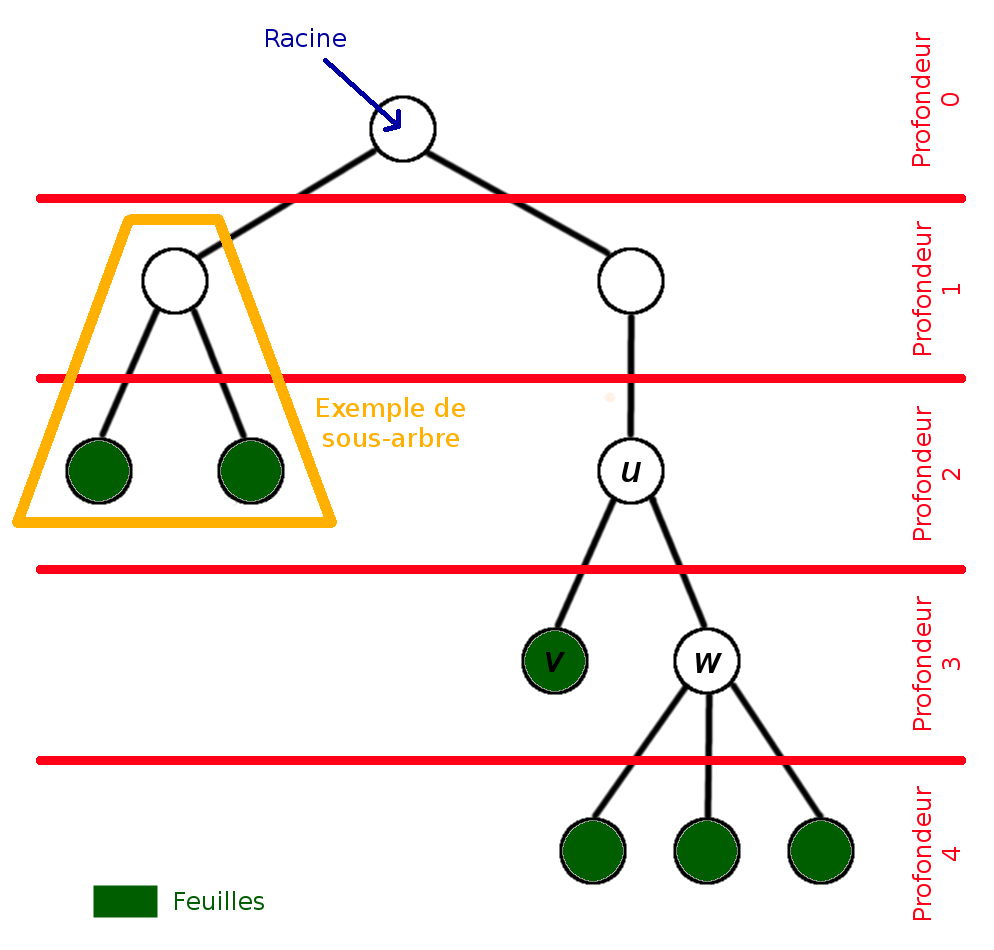
- La racine d’un arbre est un nœud arbitrairement choisi de celui-ci. Généralement, son choix est assez intuitif selon le cas d’utilisation. Par exemple, si on représente l’architecture des dossiers sous Linux par un arbre, la racine sera le dossier /; et si on modélise toutes les combinaisons possibles au jeu du morpion, la racine sera une grille de morpion vide.
- Les feuilles sont les nœuds tout en bas de l’arbre, c’est à dire les nœuds n’ayant qu’un unique voisin.
- La profondeur d’un nœud est sa distance (en nombre d’arêtes) à la racine. En particulier, la racine de l’arbre est de profondeur 0.
- La profondeur de l’arbre est la profondeur maximale parmi ses nœuds.
- On appelle parent d’un nœud v le nœud u tel que u et v sont voisins et v est à la profondeur de u plus 1.
- On appelle enfants d’un nœud u les nœuds v, w… tel que u est voisin de v, w… et u est à la profondeur de v, w… moins 1.
- On appelle sous-arbre (de racine u) un sous-ensemble des nœuds de l’arbre incluant tous les enfants, petits-enfants (etc.) de u. Par construction, un sous-arbre est aussi un arbre.
Voici un exemple d’un même arbre, donné pour deux choix de racines différentes. Il est intéressant de noter que la profondeur de l’arbre n’est pas forcément la même selon la racine :
 |
 |
L’arbre de droite (contrairement à celui de gauche) est dit équilibré, c’est à dire que chacune de ses feuilles est à la même profondeur (à +1 ou -1 près).
Enfin, on appelle arbre couvrant d’un graphe l’arbre tel que chaque nœud du graphe apparaît une unique fois dans l’arbre, et tel que deux nœuds adjacents dans l’arbre le sont aussi dans le graphe. Bien évidemment, il peut y avoir plusieurs arbres couvrants associés à un même arbre, selon le choix de la racine, et de l’ordre dans lequel les nœuds sont parcourus.
Les arbres et le morpion
Les arbres sont très pratiques pour représenter de nombreuses choses. Si on part par exemple d’une grille de morpion vide, et qu’on énumère les possibilités de parties, on obtient un graphe sous la forme d’un arbre :
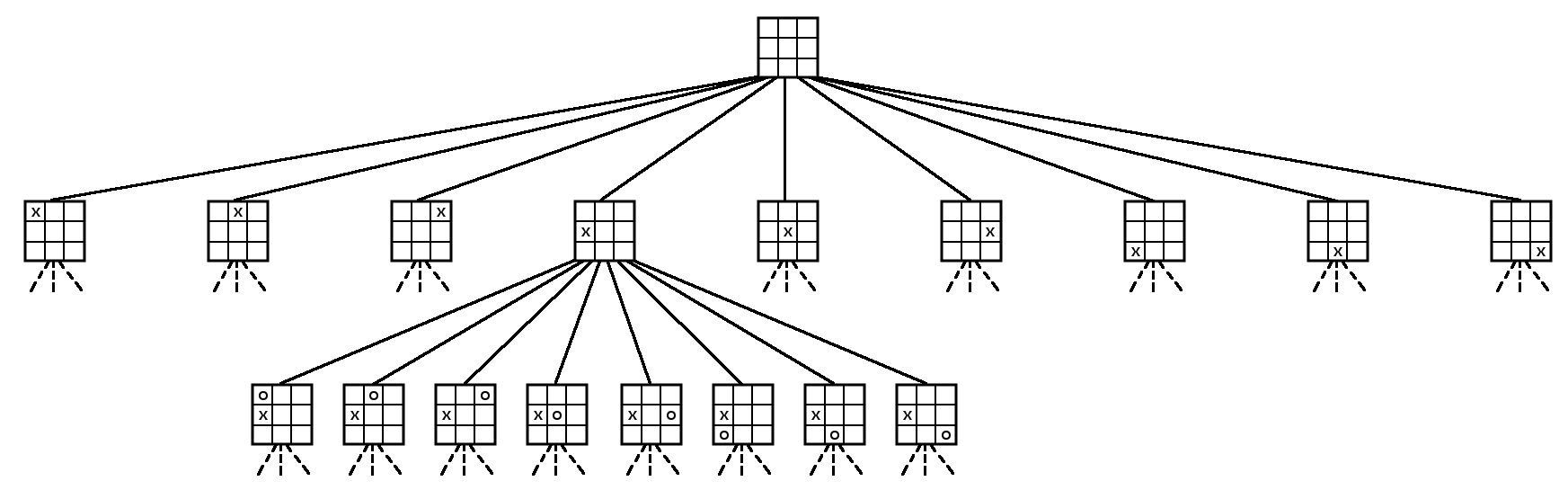
Ainsi, chaque branche de l’arbre représente une partie complète de morpion, et énumérer toutes les parties revient à calculer tout l’arbre.
Il est à noter que calculer tout l’arbre prend beaucoup de temps et de mémoire pour des cas plus complexe. Déjà, dans le cas du morpion, on aura 9! nœuds dans l’arbre. En pratique, on va souvent explorer un arbre à la volée, c’est à dire en explorant toutes ses branches mais sans stocker toute la structure de l’arbre.
Les arbres binaires de recherche
Un arbre binaire de recherche est une structure sous forme d’arbre, à laquelle on ajoute une fonction d’étiquetage qui à chaque nœud associe une étiquette, c’est à dire un élément d’un ensemble (généralement un entier) munie d’un opérateur de comparaison (< pour les entiers).
Le point particulier de cette structure est qu’elle est construite (et modifiée) de telle sorte que les labels sont toujours triés dans l’ordre croissant (selon la relation d’ordre associée à l’ensemble sur lequel sont définies les étiquettes). Plus exactement, on a la structure suivante :
- Chaque noeud soit est une feuille, soit a au plus deux enfants (d’où le mot binaire dans le nom de la structure).
- Soit un nœud u n’étant pas une feuille, et ayant deux enfants v (branche de gauche) et w (branche de droite), alors tout nœud dans le sous-arbre de racine v a un label inférieur à celui de u. De même, tout nœud dans le sous-arbre de racine w a un label supérieur à celui de u.
L’intérêt d’une telle organisation est qu’il est très simple (et rapide) de retrouver un nœud de label connu : en partant de la racine, on descend progressivement dans le sous-arbre de gauche ou de droite selon le résultat de l’opérateur de comparaison. De même, il est rapide de vérifier si un label existe dans l’arbre.
La complexité des arbres binaires de recherche réside dans la suppression d’un élément. En effet, il faut veiller à conserver la structure de l’arbre, sinon il ne pourra plus servir par la suite. Nous n’entrerons pas dans ces détails ici, mais il est important de garder à l’esprit que la suppression d’éléments au sein d’un arbre binaire de recherche a un certain coût.
Pour approfondir
- Un cours plus complet sur les arbres
- La page de OpenClassrooms sur les arbres binaires de recherche.
- La page de Wikipédia sur les arbres binaires de recherche (donne entre autres des détails sur l’insertion et la suppression d’éléments)
- La page de Wikipédia sur les arbres rouge-noir
